Hydrangea

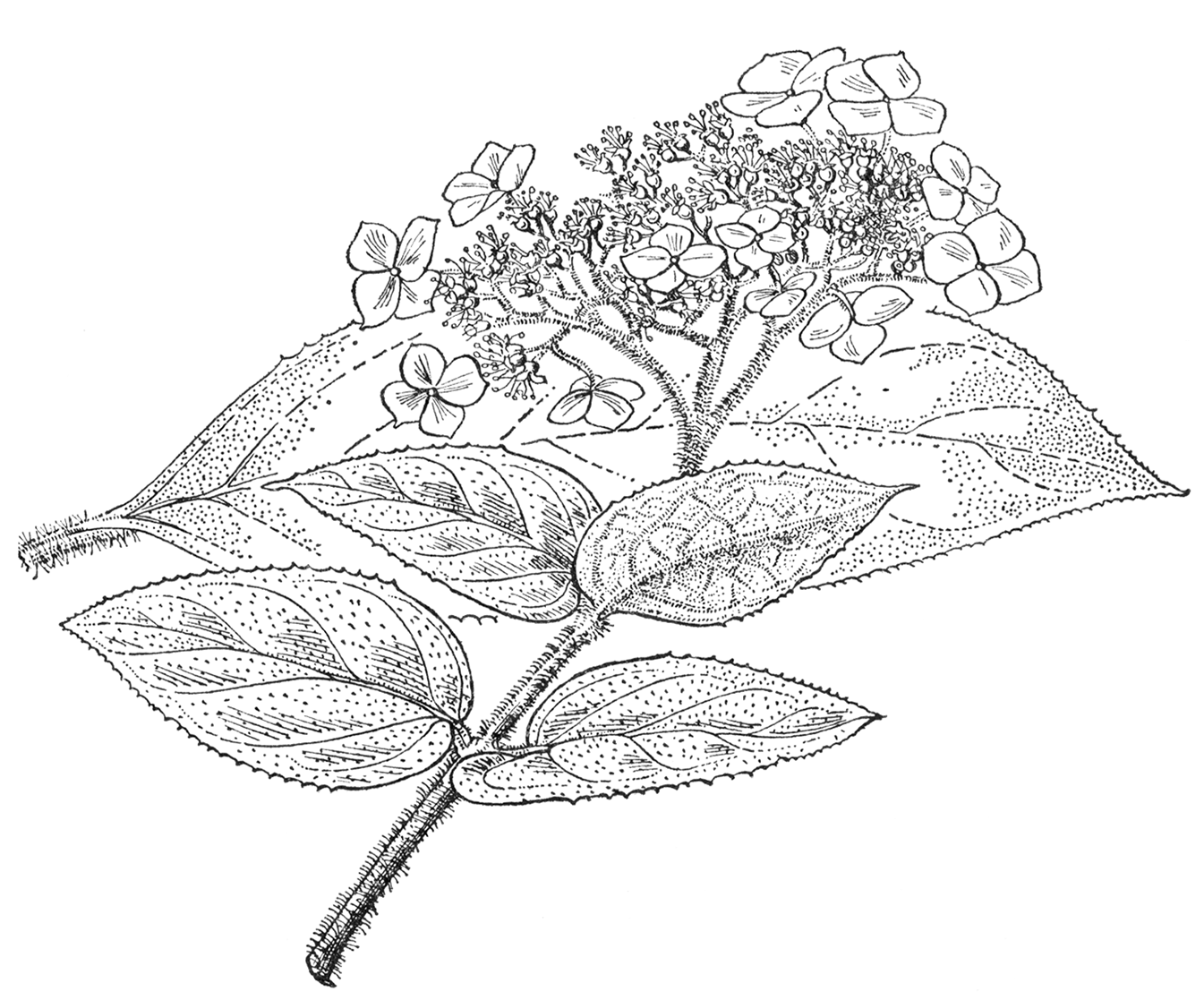
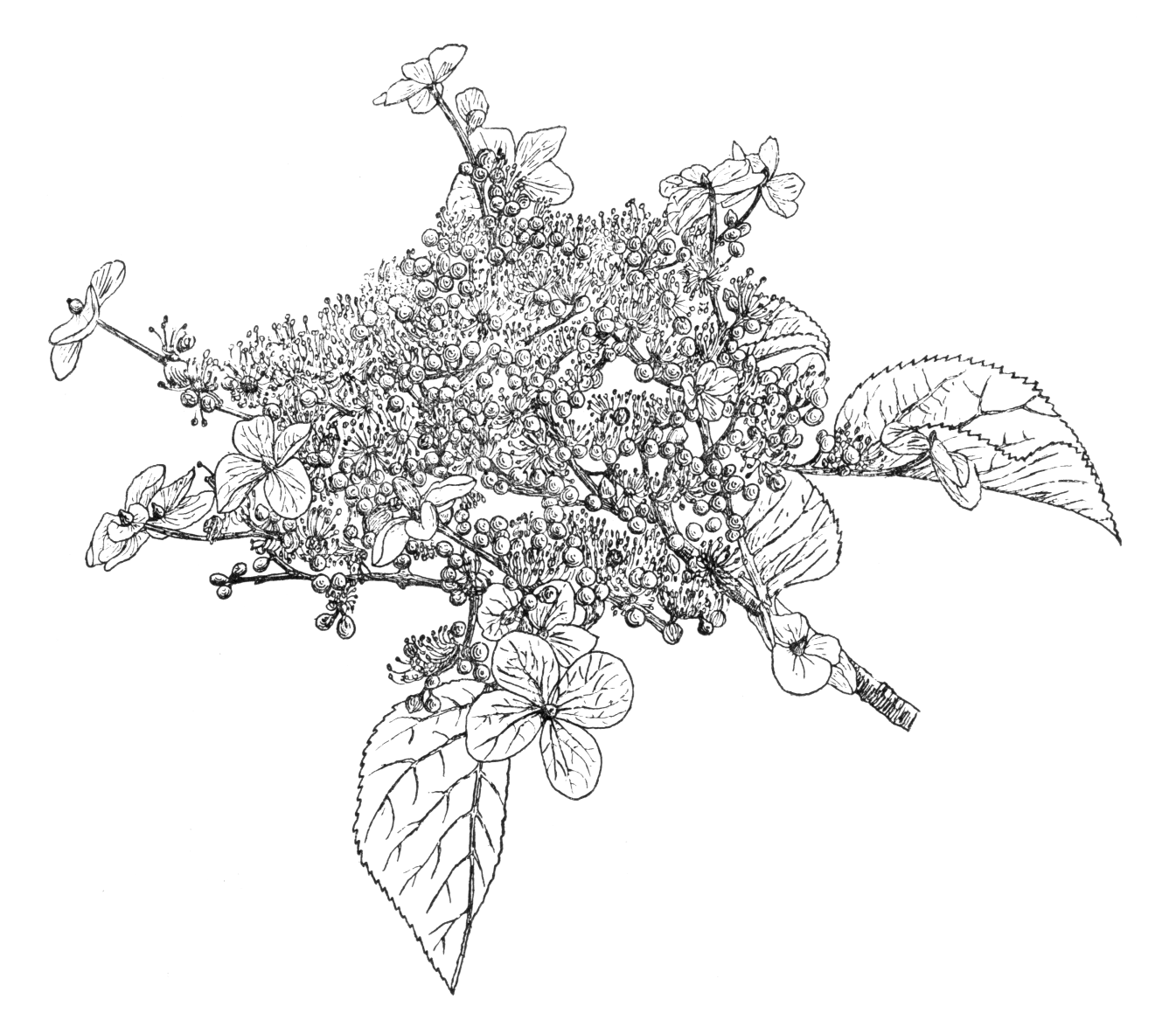
A small genus of shrubs, small trees, and climbers, represented in cultivation almost wholly by species of the typical section (section Hydrangea), which is confined to N. America, E. Asia, and the Philippines. In this group the leaves are deciduous and the inflorescence is not enclosed by bracts in the bud-stage (except in H. involucrata). In the section Cornidia, with twelve species in Central and S. America, the Philippines, and Formosa, the leaves are evergreen and the inflorescence is enclosed in the bud-stage by large ovate bracts. Of the hydrangeas grown outside in this country only H. serratifolia (integerrima) belongs to this section. In both sections the leaves are opposite. The inflorescence is corymbose (but paniculate in H. paniculata and H. quercifolia), composed of numerous fertile flowers and, in the majority of species, of a few showy sterile flowers (also known as ray-flowers). In the fertile flowers the sepals are very small and inconspicuous; the petals are four or five in number, white, blue, or pink; stamens normally eight or ten. Ovary partly or wholly enclosed in the receptacle, with usually two to four styles. The sterile flowers are usually arranged around the outside of the inflorescence and their most conspicuous feature is the large calyx, with three to five petal-like sepals. Normally the other parts of these sterile flowers do not develop, and even if petals, stamens, and ovary are formed (as is often the case among the hortensias), they rarely if ever produce seeds. In some species mutants occur in which the majority or at least a large proportion of the flowers are of the sterile type (see H. arborescens, H. paniculata, and H. macrophylla).

All the species need a good garden soil and resent dryness at the root, in areas of low rainfall hydrangeas are best planted where they are shaded from the hottest sun. The late Sir Frederick Stern found that in the dry chalky soil of his garden at Highdown the species that thrive best are H. aspera (villosa) and H. involucrata ‘Hortensis’. Most of the hydrangeas are easily increased by cuttings made of moderately ripe summer wood, but layering is often used for large-leaved species such as H. aspera, H. sargentiana, and H. quercifolia, and also for the climbing H. petiolaris. H. paniculata and H. arborescens (and its subspecies) may be lightly pruned in spring (but see further under H. paniculata ‘Grandiflora’).

The standard botanical treatment of the genus is: Elizabeth McClintock, A Monograph of the Genus Hydrangea (1957). In this excellent work a number of species familiar in gardens are reduced to the level of subspecies or sunk altogether. In the treatment that follows some species reduced by Miss McClintock have been maintained, but only where there is taxonomically some room for manoeuvre. For example, it is arguable that H. petiolaris and H. sargentiana are distinct enough from H. anomala and H. aspera respectively to merit specific rank, and they are retained here, though in truth more for the convenience of gardeners and nurserymen than from any conviction that Miss McClintock’s decision to reduce them to the rank of subspecies is wrong. On the other hand, it would be preposterous to attempt to maintain the specific identity of H. cinerea and H. radiata, which are barely more than states of the variable H. arborescens.

The standard horticultural work on the genus is: M. Haworth-Booth, The Hydrangeas (Ed. 2, 1955). His taxonomic and nomenclatural treatment of H. macrophylla and H. serrata is highly controversial and is not followed here. Nevertheless, Mr Haworth-Booth has done much to popularise in gardens many beautiful hydrangeas which were largely unknown or ignored until he brought them to notice.

From the Supplement (Vol.V)

A revised edition of Michael Haworth-Booth’s The Hydrangeas was published in 1984.